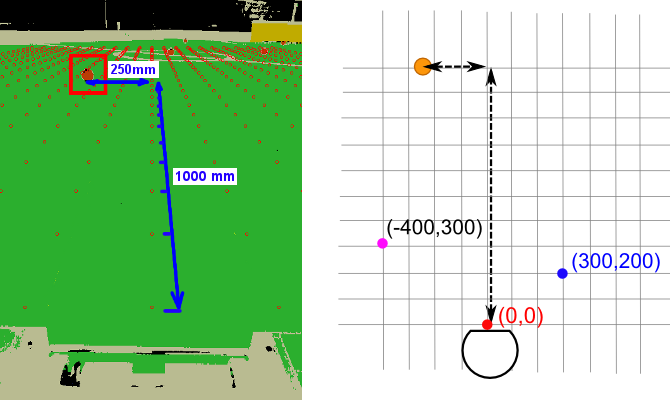
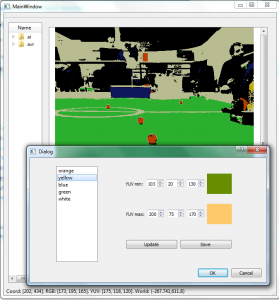
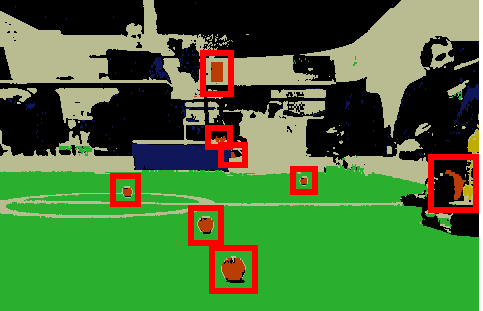
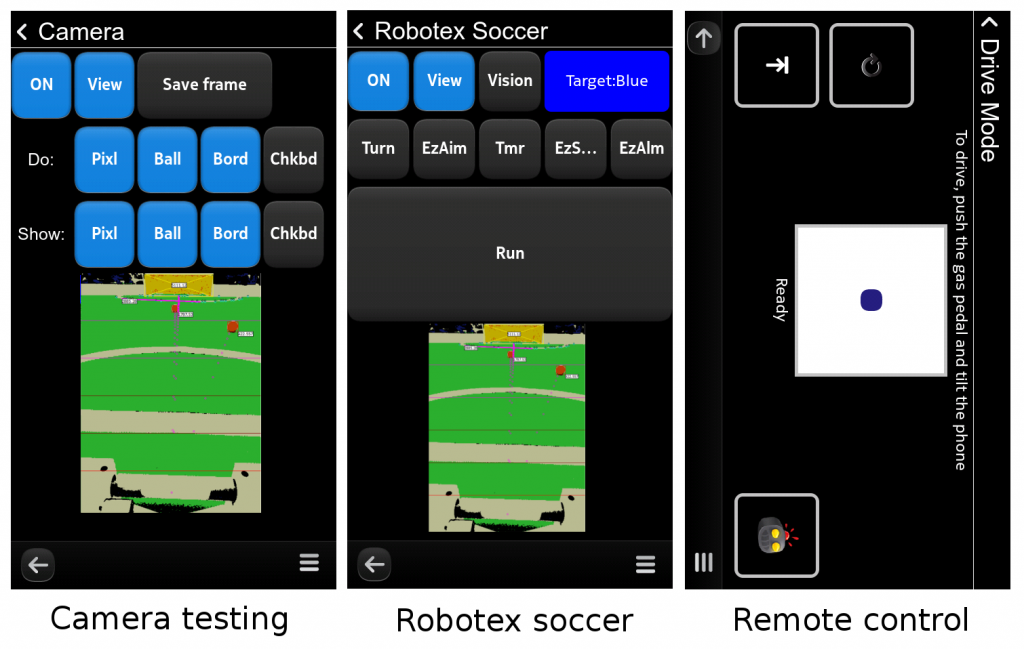
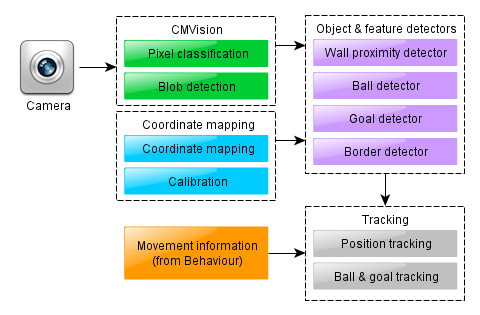
The pixel classifier/blob detector and the coordinate mapper modules, described in the previous posts establish a solid base for solving the central task of our vision processing system – object recognition. Due to the color-coding, a large part of this task is already solved by the blob detector. Indeed, every blob of orange color should be regarded as a candidate ball and every blob of blue or yellow – a candidate goal. Two things remain to be done: 1) we need to filter out “spurious” blobs (i.e. those that do not correspond to balls or goals) and 2) we need to extract useful features such as the position of the ball(s) or location of the goalposts.

Finding actual balls and goals among the candidates

So how do we discern a “spurious” orange blob from the one corresponding to a ball. Most contemporary state of the art computer vision methods, which deal with the task of classifying objects on an image, approach the problem by first extracting a number of features and then making the decision based on those. The features can be anything ranging from “average color” to “is this pixel a corner” to “whether there is a green stain in the vicinity”. Interestingly, it is believed that human visual perception works in a similar manner – by first extracting simple local features from the picture and then combining them in order to detect complex patterns. By observing the picture on the right, for example, one can get convinced that the existence of the four local “corner” features on an image is sufficient to strongly mislead the brain into believing that a complete square is present there.

The choice of appropriately selected features is therefore of paramount importance for achieving accurate object recognition. The task is complicated by the fact that we want the computation to be fast. The problem of finding a set of easy to compute features, which are, at the same time, sufficiently informative for recognizing Robotex balls and goals is highly specific to Robotex. Hence, there are no nice and easy “general”, reusable solutions. Those have to be found in a somewhat ad-hoc manner, by taking pictures of the actual balls and goals at various angles and experimenting with different options until a suitable accuracy is achieved. In fact, each of the Tartu teams came up with their own, slightly different take on the object recognition problem and all of them seemed to work well enough. In the following we present our team’s approach and this should be regarded as an example of one of many equivalently reasonable possibilities. In no way is it optimal, but it did well enough in most practical situations and at the competition.

Features for object recognition

For both ball and goal recognition (in other words, for filtering spurious blobs) we used four kinds of features (or filters): blob area, coordinate mapping, neighboring pixels and border detection. Let’s discuss those in order:

Blob area and size provides a simple criteria to filter out unreasonably small or large blobs. For the case of goal detection it is especially relevant, as we know that even when seen from far away and covered by an opponent, the goal must still be visible as a fairly large piece of color. Also, at the very end of our filtering procedure, if we still had several “candidate goals”, we would retain just the largest of the two.

Coordinate mapping is the second most obvious technique. We map the blob’s lower central pixel coordinates using our coordinate mapper to detect its hypothetical coordinates in the real world. If those are not within the playing field, we can safely discard the blob as a false positive. An additional useful test is to map the width and the height of the blob to its corresponding world dimensions. If those do not match the expected size, discard the blob. For example, a ball should not be larger than 10cm in height, even accounting for coordinate mapping errors, and a goal may not be smaller than 5 cm, etc.

The two filters above will do a fairly good job of hiding most of the irrelevant blobs, yet they will be helpless if a feature of an opponent’s robot (such as a red LED or a motor) resembles an actual tiny ball. A nice way for filtering those cases is looking at neighboring pixels. We simply count the proportion of non-green and non-white pixels directly around an orange blob (to be more precise, around the rectangle, encompassing it). If this proportion is suspiciously low, we conclude that this can’t be a valid playing ball.

Finally, we must still be able to filter out spurious ball- and goal-like objects lying outside the field boundaries. A method that we call “border locator” turned out invaluable here. Our border locator procedure starts at the pixel with the world coordinates (0, 0), that is, directly in front of the robot, and then moves in the direction of an object of interest (e.g. a candidate ball), by making steps of a fixed length (e.g. 8cm in world coordinates) and probing the corresponding pixels. If 5 of those pixels in a row happen to be non-green before the target pixel is reached, we conclude that the edge of the field is separating us from the object. The procedure is not perfect – if we are looking at a ball directly along a white line, the border locator will report it to be “outside the borders”. However, such situations are rare enough so we ignored those.

Note that all of the checks described above are very efficient. Indeed, the blob area and coordinate mapping checks require essentially around ten or so comparisons. The scan of neighboring pixels is also fast, because it suffices to check at most a 100 pixels or so, spread out equally along the border. Finally, in the border location procedure with a step size of 8cm we are guaranteed to either reach the object or hit a white border in approximately 5m/0.08 = 62 steps. Consequently, we spend at most 200 steps in total to analyze each candidate blob – way less, typically. Comparing to a single pass over the whole image (which requires examining 640×480 = 307 000 pixels) this is nothing.

Extracting useful features

After we have filtered out the spurious blobs, we do some post-processing. For the balls, we do the following:

• Check whether at least 75% of the neighboring pixels are white. If so, we mark the ball as being probably “near a wall”. Grabbing such balls is more complicated than others, so our algorithm ignores those in the beginning of the game.
• Check whether the ball’s blob lies within a goal’s blob. If so, we mark the ball as being “in the goal”, which means we do not need to bother about it. This is not a very precise criteria, of course, but it works surprisingly well in 99% of cases.
• We also label the blob as being a potential group of several balls (rather than just one ball) if its dimensions suggest so. This is, however, an imprecise test, which was never ever needed in practice.

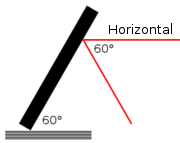
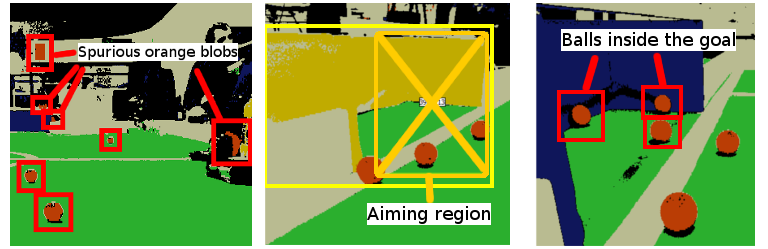
For the goals, we have to detect the situation where we see the goal at an angle, which means our aiming region can not be bluntly chosen to be the whole blob (see figure above). This particular task has been on of the trickiest of the whole vision processing and after trying numerous (fairly involved) approaches we ended up with the following unexpectedly stupid yet fast and working method:

• Split the rectangle encompassing the putative goal into two halves, left and right.
• Sample 200 pixels randomly from each half and count how many of those are green.
• If the proportion of green pixels in one of the halves is greater than in the other, presume we are viewing the goal at an angle and have to aim at the “greener” half.

Summary and code

The modules of our vision system that we have just discussed actually look as follows:

class BallDetector {
public:
    // Construct a Ball detector object, providing references
    // to all the necessary components
    BallDetector(const CMVProcessor& cmv,
                 const CoordinateMapper& cmapper,
                 const GoalDetector& goalDetector,
                 const WallProximityDetector& wallProximity);

    void processFrame();    // Extract visible balls from frame
    void paint(QPainter* painter) const; // Paint for debugging

    QList<Ball> balls;      // Detected balls

protected:
    // Main filtering method:
    // Given a blob rectangle, checks whether it contains a ball
    Ball checkBall(const QRect& rect, int area) const;

    // ... some details omitted ... //
};

class GoalDetector {
public:
    GoalDetector(const CMVProcessor& cmv,
                 const CoordinateMapper& cmapper,
                 const WallProximityDetector& wallProximity);

    void processFrame();                 // Extract visible goals
    void paint(QPainter* painter) const; // Paint for debugging

    Goal yellow;    // Detected yellow goal (if any)
    Goal blue;      // Detected blue goal (if any)

protected:
    // Main method:
    // Given a rect, checks whether it is a valid goal
    Goal checkGoal(const QRect& rect, bool yellow, int area);

    // ... some details omitted ... //
};

class BorderLocator {
public:
    BorderLocator(const CMVProcessor& cmv,
                  const CoordinateMapper& cmapper);

    // Shoots a probe at a specific point in world coordinates
    // Returns a BorderProbe object with shot results
    BorderProbe shootAtPoint(QPointF worldPoint) const;

protected:
    // ... omitted ... //
};

An attentive reader will notice the WallProximityDetector module mentioned in the code. We shall come to it in a later post.

Knowing that a certain orange blob on the picture corresponds to a ball does not help us much unless we know how to drive in order to reach it. In order to be able to do that, we must compute where exactly this ball is located with respect to the robot. Thus, the second important basic component of our vision subsystem (after the color recognition/blob detection module) is the coordinate mapper.

We shall assign coordinates to the points of the field. Coordinates will be local to the robot (we shall therefore refer to them as “robot frame coordinates“). That means, the origin of the coordinate system (the point (0, 0), red on the image above) will will be fixed directly in front of the robot. The point with coordinates (300, 200) will be 300mm to the right and 200mm to the front (the blue point on the image above), etc.

With the coordinate system fixed, each pixel on the camera frame uniquely corresponds to a point on the field with particular coordinates. The task of the coordinate mapper is to convert from pixel coordinates to robot frame coordinates and vice-versa.

Camera projection

How do we perform the conversion? Let’s start with the distance, i.e. the Y coordinate. If you examine the typical view from our robot’s camera, you will easily note that the vertical coordinate of a pixel uniquely determines its distance from the robot. Points on the “horizon line” lie at infinite distance, and become closer as you move lower along the picture. The relation between the pixel’s vertical coordinate (counted from the horizon line) and actual distance to it is an inverse function:

ActualDistance = A + B/PixelVerticalCoord,

where A and B are some constants.

I will not bore you with the proof of this fact. If you are really interested, however, you should be able to come up with it on your own after reading a bit about the pinhole camera model, the perspective projection, and meditating on the following figure (here, p is the pixel vertical coordinate as counted from the horizon line and d is the actual distance on the ground).

Finding the X coordinate (i.e. the distance “to the right”) is even easier. Note that as you approach horizon, the pixel-width of a, say, 100mm segment, decreases linearly.

That means that the relation between a pixel’s horizontal coordinate and the corresponding point’s coordinate on the ground must be of the form:

ActualRight = C * PixelRight / PixelVerticalCoord

where C is some constant again.

Finding the constants

Once we’re done with the math, we need to find the constants A, B, C as well as the pixel coordinate of the horizon line to make the formulas work in practice. Those constants depend on the orientation of the camera with respect to the ground, i.e. the way the camera is attached to the robot. For robots that have their cameras rigidly fixed it is typically possible to compute those values once and forget about them. Telliskivi’s camera, however, is not rigidly fixed, because the smartphone can be taken out from the mount. Thus, every time the phone is repositioned (or simply nudged hard enough to get displaced), we need to recalibrate the coordinate mapper by computing the A, B and C values, corresponding to the new phone orientation.

To do the calibration, we need to “label” some pixels on the screen with their actual coordinates in the robot frame. The easiest approach for that is to lay out a checkerboard pattern (or any other easily detectable pattern) printed on a piece of paper in front of the robot. After that, a simple corner detection algorithm can locate the pixels, which correspond to the four corners of the pattern. As the dimensions of the pattern are known and it is laid out at a fixed distance from the robot’s front edge, the actual coordinates, corresponding to the corner pixels are also known. Hence, putting those values into the equations above lets us compute the suitable values for the A, B and C constants and this completes the calibration.

On coordinate mapping precision

It is worth keeping in mind that due to the properties of perspective projection, coordinates of faraway objects computed using the formulas presented above can be rather imprecise. Indeed, for objects further than 3-4 meters, an error by a single pixel can correspond to a distance error of more than 20 cm. Such pixel errors, however, happen fairly often. For example, a shadow may confuse the blob detector to not include the lower part of a ball into the blob. Alternatively, the robot itself may tilt or vibrate due to the irregularities of the ground – this shakes the camera and shifts the whole picture by a couple of pixels back and forth. Luckily, this discrepancy is usually not an issue as long as our main goal is chase balls and kick them into goals. If better precision for faraway objects were necessary, however, it would be possible to achieve by carefully tracking the objects over time and averaging the measurements.

Summary

To summarize, this is how the actual declaration of our coordinate mapping module looks like (as usual, with a couple of irrelevant simplifications):

class CoordinateMapper {
private:
    // Mapping parameters we've discussed above
    qreal A, B, C;
    // Screen coordinates of the midpoint of the horizon line
    QPointF horizonMidPoint;
public:
    // Load parameters from file / Save to file
    void load(const QString& filename);
    void save(const QString& filename) const;

    // Initialize parameters from the four pixel coordinates
    // of a predefined pattern lying in front of the robot.
    bool fromCheckerboardPattern(QPoint bottomLeft, QPoint topLeft, 
                                 QPoint bottomRight, QPoint topRight);

    // The main conversion routines
    QPointF toRobotFrame(const QPointF& screen) const;
    QPointF toScreen(const QPointF& robotFrame) const;

    // Paints a grid of points visualizing current mapping
    // (you've seen it on the pictures above).
    // Useful for debugging.
    void paint(QPainter* painter) const;
};

In addition, we also have a CheckerboardDetector helper module of the following kind:

class CheckerboardDetector {
public:
    void init(QSize size);                 // Initialize module
    void processFrame(const uyvy* frame);  // Detect pattern
    void paint(QPainter* painter) const;   // Debug painting

    bool failed() const;                   // Was detection successful?
    const QPoint& corner(CornerId which) const; // Detected corners
    enum CornerId { TOPLEFT, TOPRIGHT, BOTTOMLEFT, BOTTOMRIGHT };
private:
    // ... omitted ...
}

The task of the vision processing module is to detect various objects on the camera frame. In its most general form, this task of computer vision is quite tricky and is still an active area of research. Luckily, we do not need a general-purpose computer vision system for the Robotex robot. Our task is simpler because the set of objects that we will be recognizing is very limited – we are primarily interested in the balls and the goals. In addition, the objects are color-coded: the balls are orange, the goals are blue and yellow, the playing field is green with white lines, and the opponent is not allowed to color significant portions of itself into any of those colors.

Making good use of the color information is of paramount importance for implementing a fast Robotex vision processor. Thus, the first step in our vision processing pipeline takes in a camera frame and decides, for each pixel, whether the pixel is “orange“, “white“, “green“, “blue“, “yellow” or something else.

Recognizing colors

Firstly, let me briefly remind you, that each pixel of a camera frame represents its actual color using three numbers – the color’s coordinates in a particular color space. The most well-known color space is RGB. Pixels in the RGB color space are represented as a mixture of “red”, “green” and “blue” components, with each component given a particular weight. Pixel (1, 0, 0) in the RGB space corresponds to “pure bright red”. Pixel (0, 0.5, 0) – “half-bright green”, and so on.

Most cameras internally use a different color space – YUV. In this color space, the first pixel component (“Y”) corresponds to the overall brightness, and the two last components (“UV”) code the hue. The particular choice of the color space is not too important, however. What is important is to understand that our color recognition step needs to take each pixel’s YUV color code and determine which of the five “important” colors (orange, yellow, blue, green or white) it resembles.

There is a number of fairly obvious techniques one might use to encode such a classification. In our case we used the so-called “box” classifier, due to the fact that it is fast and its implementation was available. The idea is simple: for each target color, we specify the minimum and maximum values of the Y, U and V coordinates that a pixel must have in order to be classified into such target color. For example, we might say that:

Orange pixels:  (30, 50, 120) <= (Y, U, V) <= (160, 120, 225)
Yellow pixels: (103, 20, 130) <= (Y, U, V) <= (200, 75, 170)
... etc ...

How do we find the proper “boxes” for each target color? This task is trickier than it seems. Firstly, due to different lighting conditions the same orange ball may have different pixel colors on the frame.

Secondly, even for fixed lighting conditions, the camera’s automatic color temperature adjustment control may sometimes drift temporarily, resulting in pixel colors changing in a similar manner. Thirdly, shadows and reflections influence visible color: as you might note on the picture above, the top of the golf ball has some pixels that are purely white, and the bottom part may have some black pixels due to the shadow. Finally, rapid movements of the robot (rotations, primarily) make the picture blurry and due to this, the orange color of the balls may get mixed with the background, resulting in something not-truly-orange anymore.

Consequently, the color classifier has to be calibrated for the specific lighting conditions. Such calibration can, in principle, be made automatically by showing the robot a printed page with a set of reference colors and having it adjust its pixel classifier in accordance. For the Telliskivi project we did not, unfortunately, have the time to implement such calibration reliably, and instead used a simple manual tool for tuning the parameters. Thus, whenever lighting conditions changed, we had to take some pictures of the playing field and then play with the numbers a bit to achieve satisfactory results. This did get somewhat annoying by the end.

After we have found the suitable parameters, implementing the pixel classification algorithm is as easy as writing a single for-loop with a couple of if-statements. It is, however, possible, to implement this classification especially efficiently using clever bit-manipulation tricks. Best of all, such algorithm has been implemented in an open-source (GPL) library called CMVision. The algorithm and the inner workings of the library are well-described in a thesis by its author, J. Bruce. It is a worthy reading, if you ever plan on using the library or implementing a similar method.

Blob detection

Once we have classified each pixel into one of the five colors, we need to detect connected groups (“blobs”) of same colored-pixels. In particular, orange blobs will be our candidate balls and blue and yellow blobs will be candidate goals.

An algorithm for such blob detection is not trivial enough for me to go into describing it here, but it is no rocket science – anyone who has done an “Algorithms” course should be capable of coming up with one. Fortunately, the CMVision library already implements an efficient blob detector (look into the above mentioned thesis for more details).

Why not OpenCV?

Some of you might have heard the name of OpenCV – an open-source state of the art computer vision algorithm library. It is widely used in robotics and several Robotex competitors did use this library for their robots. I have a strong feeling, however, that for the purposes of Robotex soccer this is not the best choice. OpenCV is primarily aimed at “more complex” and “general purpose” vision processing tasks. As a result, most of its algorithms are either not enormously useful for our purposes (such as contour detection and object tracking), or are too general and thus somewhat inefficient. In particular, the use of OpenCV would impose a pipeline of image filters, where each filter would require a full pass over all pixels of the camera frame. This would be a rather inefficient solution (we know it from the fellow teams’ experience). As you shall see in the later posts, all of our actual object recognition routines can be implemented much more efficiently without the need to perform multiple full passes over the image.

Summary

We have just presented you the idea behind the first module of our vision processing system. The module is responsible for recognizing the colors of the pixels in the frame and detecting blobs. In our code the module is implemented as (approximately) the following C++ class, which simply wraps the functionality of the CMVision library.

class CMVProcessor {
public:
  CMVision cmvision; // Instance of the cmvision class

  CMVProcessor(const PixelClassifierSettings& settings);
  void init(QSize size);          // Initialize cmvision
  void processFrame(uyvy* frame); // Invoke cmvision.processFrame()
  void paint(QPainter* painter) const; // Paint the result (for debugging)
};

Now that we are done with the hardware details, let us move to the “brain” of the Telliskivi robot – the software, running on the smartphone. By now you can safely forget everything you read (if you did) about the hardware, and only keep in mind that Telliskivi is a two-wheeled robot with a coilgun and a ball sensor, that can communicate over Bluetooth.

You should also know that Telliskivi’s platform understands the following simple set of textual commands:

• speeds <x> <y>   – sets the PID speed setpoints for the two motors. In particular, “speeds 0 0” means “stop moving”, “speeds 100 100” means “move forward at a maximum speed”, “speeds 10 -10” means “turn clockwise on the spot”,
• charge – enables the charging of the coilgun capacitor,
• shoot – shoots the coilgun,
• discharge – gracefully discharges the coilgun capacitor,
• sense – returns 1 if the ball is in the detector and 0 otherwise.
  (*Actually, things are just a tiny bit more complicated, but it is not important here).

We now add a smartphone to control this plaform. The phone will use its camera to observe the surroundings and will communicate with the platform telling it where to go and when to shoot in order to win at a Robotex Soccer game.

The software that helps Telliskivi to achieve this goal is structured as follows:

The Robot Controller

The Robot Controller is a module (a C++ class) which hides the details of Bluetooth communication (i.e. the bluez library and the socket API). The class has methods which correspond to the Bluetooth commands mentioned above, i.e. “speeds(a,b)“, “charge()“, “shoot()” and “sense()” and “discharge()“. In this way the rest of the system does not have to know anything at all how exactly the robot is controlled.

For example, a simple change in this class lets us use the same software to control a Lego NXT platform instead of Telliskivi. That platform does not have a coilgun nor a ball sensor (hence the shoot(), sense() and discard() methods do not do anything), but it can move in the same way, so if we let our soccer software run with the NXT robot, the robot still manages to imitate playing soccer – it would approach balls and desperately try to push them towards the goal. Looks funny and makes you wonder whether it is polite to laugh at physically disabled robots.

Obviously, the robot controller is the first thing we implemented. We did it even before we had Telliskivi available (we could use the Lego NXT prototype at that time).

Graphical User Interface (GUI)

The GUI is the visual interface of the smartphone app. Ours is written in QML, a HTML-like language for describing user-interfaces. Together with the Qt framework this is the recommended way of making user applications for Nokia N9. It takes time to get used to, but once you grasp it, it is fairly straightforward.

The overall concept of our UI is not worth delving deeply into – it is just a bunch of screens organized in a hierarchical manner. Most screens are meant for debugging – checking whether the Bluetooth connection works, whether the robot controller acts appropriately, whether the vision system detects objects correctly, and whether the various behaviours are behaving as expected.

In addition, there is one “main competition” screen with a large “run” button, that invokes the Robotex soccer mode and two “remote control” screens. One allows to use the phone as a remote control for the Telliskivi platform and steer it by tilting the phone (this is fun!). Another screen is meant to be used as a VNC server (so that you can log in to the robot remotely over the network from you computer, view the camera image and drive around – even more fun). For the curious, here are some screenshots:

Vision Processing

The vision processing sybsystem is responsible for grabbing the frames from the camera (using QtMultimedia), and extracting all the necessary visual information – detecting balls, goals and walls. In our case, parts of the vision subsystem were also responsible for tracking the robot’s position relative to the field. Thus, it is a fairly complex module with multiple parts and we shall cover those in more detail in later posts.

Behaviour Control

The last part is responsible for processing vision information, making decisions based on it, and converting them into actual movement commands for the robot – we call it the “behaviour controller”.

As the camera was the main sensor for our robot, we had the behaviour controller synchronized with the camera frame events. That is, the behaviour controller’s main method, (called “tick”), was invoked on each camera frame (which means, approximately 30 times per second). This method would examine the new information from the vision subsystem and act in correspondence to its current “goal”, perhaps changing the goal for the next tick if necessary. This can be written down schematically as the following algorithm:

on every camera frame do {
   visionProcessor.processFrame();
   currentGoal = behave(currentGoal, visionProcessor, robotController);
}

In a later post we shall see how depending on the choice of representation of the “goal”, this generic approach can result in behaviours ranging from a simple memoryless single-reflex robot, to somewhat more complex state machines up to the more sophisticated solutions, suitable for the actual soccer-playing algorithm.

The ROS Alternative

As you might guess, all of our robot’s software was written by us from scratch. This is a consequence of us being new to the platform, the platform being new to the world (there is not too much robotics-related software pre-packaged for N9 out there yet), and the desire to learn and invent on our own. However, it does not mean that everyone has to write things from scratch every time. Of course, there is some good robotics software out there to be reused. Perhaps the most popular system that is worth knowing about is ROS (“Robot OS”).

Despite the name, ROS is not an operating system. It is a set of linux programs and libraries, providing a framework for easy development of robot “brains”. It has a number of useful ready-made modules and lets you add your own easily. There are modules for sensor access, visualization, basic image processing, localization and control for some of the popular robotic platforms. In addition, ROS provides a well-designed system for establishing asynchronous communications between the various modules: each module can run in a separate process and publish events in a “topic”, to which other modules may dynamically “subscribe”.

Note that such an asynchronous system is different from the simpler Telliskivi approach. As you could hopefully understand from the descriptions above, in the Telliskivi solution, the various parts are fairly strictly structured. They all run in a single process, and operate in a mostly synchronized fashion. That is, every camera frame triggers the behaviour module, which, in turn, invokes the vision processing and sends commands to the robot controller. The next frame will trigger the same procedure again, etc. This makes the whole system fairly easy to understand, develop and debug.

For robots that are more complicated than Telliskivi in their set of sensors and behaviours, such a solution might not always be appropriate. Firstly, different sensors might supply their data at different rates. Secondly, having several CPU cores requires you to run the code in multiple parallel processes if you want to make good use of your computing power. Even for a simpler robot, using ROS may be very convenient. In fact, several Robotex teams did use it quite successfully.

In any case, though, independently of whether the robot’s modules communicate in a synchronous or asynchronous mode, whether they are parts of a framework like ROS or simple custom-made C++ classes, whether they run on a laptop or a smartphone, the overall structure of a typical soccer robot’s brain will still be the one shown above. It will consist of the Vision Processor, the Behaviour Processor, the Robot Controller and the GUI.

Summary

To provide the final high-level overview, the diagram below depicts all of the programming that we had to do for the Telliskivi project. This comprises:

• about 800 lines of C code for AVR microcontrollers,
• about 7000 lines of C++ code for the Vision/Behaviour code
• about 2000 lines of QML code for the smartphone UI elements.
• about 900 lines of Python code for the simulator
• about 500 lines of C++ code for the Vision test application (for the Desktop)